WCSE

Trees with Given Independence Number Maximizing the A --Spectral Radius

Abstract— Spectral graph theory is a widely studied and applied subject in combinatorial mathematics, computer science and social science. Nikiforov (2017) defined a convex linear combination for the graph G , denoted by 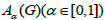 . This concept can be regarded as a common generalization of adjacency  matrix and unsigned Laplacian matrix. We mainly study the 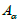-spectral extreme problem for graphs, which is a generalization of Brualdi and Solheid's problem on  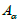-matrices. Let  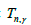be the set of all trees with order n and independence number  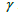. By graph transformations we determine the graphs with maximal 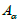-spectral radius among 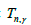for 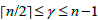. Therefore, we extend the results of Ji and Lu (2016) from spectral radius to  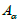-spectral radius.

Index Terms—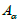-spectral radius, independence number, tree

Lei Zhang
School of Mathematics and Statistics, Qinghai Normal University, Xining, CHINA
Academy of Plateau, Science and Sustainability, Xining, CHINA
The State Key Laboratory of Tibetan Information Processing and Application, Xining, CHINA
Yuanmei Chen
School of Mathematics and Statistics, Qinghai Normal University, Xining, CHINA
Haizhen Ren
School of Mathematics and Statistics, Qinghai Normal University, Xining, CHINA
Academy of Plateau, Science and Sustainability, Xining, CHINA
The State Key Laboratory of Tibetan Information Processing and Application, Xining, CHINA

[Download]

Cite:Lei Zhang, Yuanmei Chen, Haizhen Ren, "Trees with Given Independence Number Maximizing the -Spectral Radius, " Proceedings of 2022 the 12th International Workshop on Computer Science and Engineering (WCSE 2022), pp. 248-252, June 24-27, 2022.